what is the best fuel to air ratio?
Tabular array of Contents
- Air fuel ratio definition
- Air fuel ratio formula
- Air fuel ratio for different fuels
- How stoichiometric air fuel ratio is calculated
- Lambda air fuel ratio
- Air fuel ratio and engine performance
- Air fuel ratio reckoner
- Impact of air fuel ratio on engine emissions
- Lambda airtight-loop combustion control
Air fuel ratio definition
Thermal engines use fuel and oxygen (from air) to produce energy through combustion. To guarantee the combustion procedure, certain quantities of fuel and air need to be supplied in the combustion chamber. A complete combustion takes place when all the fuel is burned, in the exhaust gas there volition be no quantities of unburnt fuel.
Air fuel ratio is defined as the ratio of air and fuel of a mixture prepared for combustion. For instance, if we have a mixture of methyl hydride and air which has the air fuel ratio of 17.v, it means that in the mixture we accept 17.5 kg of air and i kg of methane.
The ideal (theoretical) air fuel ratio, for a consummate combustion, is called stoichiometric air fuel ratio. For a gasoline (petrol) engine, the stoichiometric air fuel ratio is around 14.7:1. This means that, in order to burn down completely ane kg of fuel, we demand fourteen.vii kg of air. The combustion is possible even is the AFR is different than stoichiometric. For the combustion process to take place in a gasoline engine, the minimum AFR is around 6:1 and the maximum can go up to 20:ane.
When the air fuel ratio is college than the stoichiometric ratio, the air fuel mixture is called lean. When the air fuel ratio is lower than the stoichiometric ratio, the air fuel mixture is called rich. For example, for a gasoline engine, an AFR of xvi.5:1 is lean and 13.vii:one is rich.
Get back
Air fuel ratio formula
In the context of internal combustion engines, air fuel ratio (AF or AFR) is defined as the ratio between the mass of air ma and mass fuel thouf , used by the engine when running:
\[\bbox[#FFFF9D]{AFR = \frac{m_a}{m_f}} \tag{1}\]
The inverse ratio is called fuel-air ratio (FA or FAR) and it's calculated every bit:
\[FAR = \frac{m_f}{m_a} = \frac{1}{AFR} \tag{ane}\]
Go back
Air fuel ratio for different fuels
In the tabular array below we can run across the stoichiometric air fuel ratio for several fossil fuels.
| Fuel | Chemic formula | AFR |
| Methanol | CHthreeOH | 6.47:1 |
| Ethanol | C2HvOH | ix:1 |
| Butanol | CivH9OH | 11.2:1 |
| Diesel | C12H23 | 14.5:1 |
| Gasoline | C8H18 | 14.7:1 |
| Propane | CthreeH8 | 15.67:1 |
| Methane | CH4 | 17.19:1 |
| Hydrogen | H2 | 34.3:1 |
Source: wikipedia.org
For example, in order to burn completely one kg of ethanol, we need 9 kg of air and to burn ane kg of diesel fuel, we need fourteen.5 kg of air.
Spark ignition (SI) engines usually run on gasoline (petrol) fuel. The AFR of the SI engines varies inside the range 12:1 (rich) to 20:1 (lean), depending on the operating condition of the engine (temperature, speed, load, etc.). Modernistic internal combustion engines operate as much as possible effectually the stoichiometric AFR (mainly for gas after-treatment reasons). In the tabular array below you tin come across an case of a SI engine AFR, office of engine speed and torque.
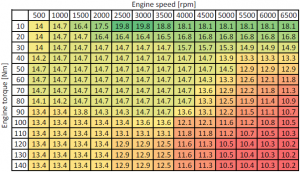
Epitome: Case of air fuel ratio (AFR) function of engine speed and torque
Pinch ignition (CI) engines usually run on diesel fuel. Due to the nature of the combustion process, CI engines always run on lean mixtures, with AFR betwixt 18:1 and 70:i. The main difference, compared with SI engines, is that CI engines run on stratified (not homogeneous) air fuel mixtures, while SI run on homogeneous mixtures (in case of port-injection engines).
The table above is entered in a Scilab script and a contour plot is generated.
EngSpd_rpm_X = [500 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000 6500]; EngTq_Nm_Y = [ten;20;30;40;50;60;70;lxxx;xc;100;110;120;130;140]; EngAFR_rat_Z = [14 xiv.7 16.4 17.5 19.eight xix.8 18.8 18.1 18.1 eighteen.i xviii.1 18.1 xviii.1; 14 14.7 14.vii 16.4 sixteen.iv 16.4 16.5 xvi.8 xvi.8 xvi.8 16.viii 16.8 16.8; fourteen 14.7 14.7 fourteen.7 14.vii 14.vii 14.7 15.7 15.7 15.iii 14.9 14.9 14.9; 14.2 14.7 14.7 14.7 xiv.7 xiv.seven 14.7 14.vii 14.7 13.9 13.three 13.3 xiii.three; 14.7 14.vii 14.7 14.7 14.7 14.7 14.7 14.7 14.seven fourteen.5 12.9 12.9 12.nine; xiv.seven xiv.7 xiv.7 xiv.7 fourteen.vii 14.7 fourteen.vii xiv.seven xiv.3 13.three 12.6 12.1 11.8; xiv.seven fourteen.7 14.7 14.seven 14.vii 14.7 xiv.7 14.vii 13.six 12.9 12.2 11.viii xi.3; 14.i xiv.two xiv.7 14.7 14.7 xiv.7 fourteen.7 fourteen.7 13.3 12.5 xi.9 11.4 x.9; 13.4 13.4 thirteen.8 14.3 14.3 fourteen.7 14.seven 13.6 13.1 12.2 11.v xi.1 ten.7; 13.4 13.four 13.four 13.four 13.four thirteen.6 thirteen.6 12.i 12.1 11.6 11.2 10.8 x.5; xiii.four xiii.4 13.4 xiii.4 xiii.1 13.one 13.1 xi.eight 11.8 xi.2 10.seven ten.5 10.three; 13.4 13.4 xiii.4 13.4 12.nine 12.9 12.5 11.6 11.iii 10.5 10.4 10.three x.2; xiii.four xiii.4 thirteen.four xiii.4 12.ix 12.9 12.5 11.6 11.three ten.5 10.4 x.3 ten.2; thirteen.4 13.4 13.4 13.4 12.9 12.9 12.5 eleven.6 11.iii 10.5 ten.4 10.3 x.2]; profile(EngSpd_rpm_X,EngTq_Nm_Y,EngAFR_rat_Z',xxx) xgrid() xlabel('Engine speed [rpm]') ylabel('Engine torque [Nm]') title('x-engineer.org') Running the Scilab instructions in a higher place will generate the following profile plot:

Image: Air fuel contour plot with Scilab
Go back
How stoichiometric air fuel ratio is calculated
In lodge to understand how the stoichiometric air fuel ratio is calculated, we need to look at the combustion process of the fuel. Combustion is basically a chemical reaction (called oxidation) in which a fuel is mixed with oxygen and produces carbon dioxide (COii), water (H2O) and free energy (heat). Take into account that, in order for the oxidation reaction to occur we need an activation energy (spark or high temperature). Likewise, the net reaction is highly exothermic (with rut release).
\[\text{Fuel}+\text{Oxygen}\xrightarrow[high \text{ } temperature \text{ (CI)}]{spark \text{ (SI)}} \text{Carbon dioxide} + \text{Water} + \text{Energy}\]
Instance i. For a meliorate agreement, let'southward look at the oxidation reaction of methane. This is a pretty common chemical reaction, since methane is the primary component of natural gas (in proportion of around 94 %).
Step 1. Write the chemical reaction (oxidation)
\[CH_4 + O_2 \rightarrow CO_2 + H_2O\]
Pace two. Balance the equation
\[CH_4 + {\color{Blood-red} 2} \cdot O_2 \rightarrow CO_2 +{\color{Blood-red} 2} \cdot H_2O\]
Step 3. Write downwards the standard atomic weight for each atom
\[ \begin{split}
\text{Hydrogen} &= 1.008 \text{ amu}\\
\text{Carbon} &= 12.011 \text{ amu}\\
\text{Oxygen} &= 15.999 \text{ amu}
\cease{split} \]
Stride iv. Summate the mass of fuel, which is 1 mol of marsh gas, fabricated upwards from 1 atom of carbon and 4 atoms of hydrogen.
\[m_f =12.011 + four \cdot 1.008 = 16.043 \text{ one thousand}\]
Step v. Summate the mass of oxygen, which consists of 2 moles, each mol made up from ii atoms of oxygen.
\[m_o =2 \cdot fifteen.999 \cdot two= 63.996 \text{ chiliad}\]
Stride 6. Calculate the necessary mass of air which contains the calculated mass of oxygen, taking into account that air contains around 21 % oxygen.
\[m_a = \frac{100}{21} \cdot m_o=\frac{100}{21} \cdot 63.996 = 304.743 \text{ chiliad}\]
Step 7. Calculate the air fuel ratio using equation (1)
\[AFR = \frac{m_a}{m_f} = \frac{304.743}{16.043} = 18.995 \]
The calculated AFR for methane is not exactly every bit specified in the literature. The difference might come from the fact that, in our example, we made several assumptions (air contains just 21 % oxygen, the products of the combustion are only carbon dioxide and water).
Case two. The same method tin be applied for the combustion of gasoline. Considering that gasoline is made up from iso-octane (C8H18), calculate the stoichiometric air fuel ratio for gasoline.
Step 1. Write the chemical reaction (oxidation)
\[C_{8}H_{xviii} + O_2 \rightarrow CO_2 + H_2O\]
Step 2. Balance the equation
\[C_{8}H_{18} + {\colour{Ruby-red} {12.5}} \cdot O_2 \rightarrow {\color{Red} 8} \cdot CO_2 +{\colour{Red} 9} \cdot H_2O\]
Step 3. Write down the standard atomic weight for each cantlet
\[ \begin{split}
\text{Hydrogen} &= 1.008 \text{ amu}\\
\text{Carbon} &= 12.011 \text{ amu}\\
\text{Oxygen} &= 15.999 \text{ amu}
\end{split} \]
Step 4. Summate the mass of fuel, which is i mol of iso-octane, made up from 8 atoms of carbon and eighteen atoms of hydrogen.
\[m_f =8 \cdot 12.011 + 18 \cdot 1.008 = 114.232 \text{ g}\]
Pace 5. Summate the mass of oxygen, which consists of 12.5 moles, each mol made up from 2 atoms of oxygen.
\[m_o =12.v \cdot fifteen.999 \cdot two= 399.975 \text{ grand}\]
Step 6. Summate the necessary mass of air which contains the calculated mass of oxygen, taking into business relationship that air contains around 21 % oxygen.
\[m_a = \frac{100}{21} \cdot m_o=\frac{100}{21} \cdot 399.975 = 1904.643 \text{ g}\]
Step seven. Calculate the air fuel ratio using equation (one)
\[AFR = \frac{m_a}{m_f} = \frac{1904.643}{114.232} = 16.673 \]
Again, the calculated stoichiometric air fuel ratio for gasoline is slightly different that the one provided in literature. Thus, the effect is acceptable since we made a lot of assumptions (gasoline contains only iso-octane, air contains just oxygen in proportion of 21 %, the only products of combustion are carbon dioxide and h2o, the combustion is platonic).
Go dorsum
Lambda air fuel ratio
We take seen what is and how to summate the stoichiometric (ideal) air fuel ratio. In reality, internal combustion engines practise not work exactly with ideal AFR, but with values shut to it. Therefore nosotros'll have an ideal and a actual air fuel AFR ratio. The ratio betwixt the actual air fuel ratio (AFRbodily) and the platonic/stoichiometric air fuel ratio (AFRideal) is called equivalence air fuel ratio or lambda (λ).
\[\bbox[#FFFF9D]{\lambda = \frac{AFR_{actual}}{AFR_{ideal}}} \tag{3}\]
For case, the ideal air fuel ratio for a gasoline (petrol) engine is xiv.7:1. If the actual/real AFR is thirteen.5, the equivalence cistron lambda will exist:
\[\lambda = \frac{13.v}{14.7} = 0.92\]
Depending on the value of lambda, the engine is told to piece of work with lean, stoichiometric or rich air fuel mixture.
| Equivalence factor | Air fuel mixture type | Clarification |
| λ < ane.00 | Rich | There is not enough air to burn completely the corporeality of fuel; afterwards combustion there is unburnt fuel in the frazzle gases |
| λ = ane.00 | Stoichiometric (ideal) | The mass of air is verbal for a complete combustion of the fuel; after combustion there is no excess oxygen in the exhaust and no unburnt fuel |
| λ > 1.00 | Lean | There is more oxygen than required to burn completely the amount of fuel; after combustion there is excess oxygen in the exhaust gases |
Depending on the type of fuel (gasoline or diesel) and the type of injection (direct or indirect), an internal combustion engine tin can function with lean, stoichiometric or rich air fuel mixtures.

Image: Ecoboost iii-cylinder directly injection gasoline engine (lambda map)
Credit: Ford
For example, the Ford Ecoboost 3-cylinder engine runs with stoichiometric air fuel ratio for idle to medium engine speed and complete load range, and with rich air fuel mixture at high speed and load. The reason for which information technology runs with rich mixture at loftier engine speed and load is engine cooling. The additional fuel (which will remain unburnt) is injected to blot rut (through evaporation), reducing this way the temperature in the combustion chamber.

Prototype: Diesel engine (lambda map)
Credit: wtz.de
A compression ignition (diesel) engine runs all the time with lean air fuel mixture, the value of the equivalence gene (λ) depending on the engine's operating point (speed and torque). The reason for this is the working principle of a diesel engine: decision-making load not through air mass (which is ever in excess) but through fuel mass (injection fourth dimension).
Remember that a stoichiometric equivalence cistron (λ = 1.00) means an air fuel ratio of 14.seven:i for gasoline engines and 14.5:i for diesel engines.
Go back
Air fuel ratio and engine performance
The engine performance in terms of power and fuel consumption is highly dependent on the air fuel ratio. For a gasoline engine, the lowest fuel consumption is obtained at lean AFR. The main reason is that there is enough oxygen bachelor to burn completely all the fuel which translates in mechanical work. On the other hand, the maximum power is obtained with rich air fuel mixtures. Equally explained earlier, putting more fuel in the cylinder at high engine load and speed, cools downwards the combustion bedchamber (through fuel evaporation and rut absorption) which allows the engine to produce maximum engine torque thus maximum power.

Image: Engine power and fuel consumption function of air fuel ratio (lambda)
In the figure above we can see that we can not get the maximum power of the engine and the lowest fuel consumption with the same air fuel ratio. The everyman fuel consumption (best fuel economy) is obtained with lean air fuel mixtures, with an AFR of fifteen.4:ane and an equivalence cistron (λ) of one.05. The maximum engine power is produced with rich air fuel mixtures, with an AFR of 12.half-dozen:1 and an equivalence factor (λ) of 0.86. With a stoichiometric air fuel mixture (λ = one), there is a compromise between maximum engine ability and minimum fuel consumption.
Compression ignition (diesel) engines ever run on lean air fuel mixtures (λ > 1.00). Virtually of the modernistic diesel engines run with λ between 1.65 and 1.10. The maximum efficiency (everyman fuel consumption) is obtained around λ = 1.65. Increasing the fuel amount above this value (going towards 1.10) will produce more soot (unburnt fuel particles).
In that location is an interesting study performed by R. Douglas on 2-stroke cycle engines. In his doctoral thesis "Closed Cycle Studies of a Two-Stroke Cycle Engine", R. Douglas comes with a mathematical expression of the combustion efficiency (ηλ) function of equivalence factor (λ).
For spark ignition (gasoline engine) with an equivalence gene between 0.lxxx and 1.20, the combustion efficiency is:
\[\eta_{\lambda}=-1.6082+iv.6509 \cdot \lambda – two.0746 \cdot \lambda^2 \tag{4}\]
For compression ignition (diesel engine) with an equivalence factor betwixt 1.00 and 2.00, the combustion efficiency is:
\[\eta_{\lambda}=-4.18+8.87 \cdot \lambda – 5.14 \cdot \lambda^2 + \lambda^3 \tag{five}\]
For diesel fuel engines, if the equivalence factor goes above two.00, the combustion efficiency is maximum (ane.00 or 100 %).
We can apply a Scilab script to plot the variation of the combustion efficiency function of the equivalence gene.
lmbd_g = [0.80:0.01:ane.xx]; lmbd_d = [1.00:0.01:2.00]; eff_lmbd_g = -ane.6082+iv.6509*lmbd_g-2.0746*lmbd_g.^2; eff_lmbd_d = -four.18+eight.87*lmbd_d-5.14*lmbd_d.^two+lmbd_d.^3; plot(lmbd_g,eff_lmbd_g,'b','LineWidth',2) agree plot(lmbd_d,eff_lmbd_d,'r','LineWidth',2) xgrid() xlabel('$\lambda \text{ [-]}$') ylabel('$\eta_{\lambda} \text{ [-]}$') title('x-engineer.org') fable('gasoline','diesel',four) Running the Scilab instructions above outputs the following graphical window.

Prototype: Combustion efficiency role of equivalence factor
As yous tin can see, the compression ignition (diesel) engine, at stoichiometric air fuel ratio has a very low combustion efficiency. The best combustion efficiency is obtained at λ = 2.00 for diesel and λ = 1.12 for spark ignition (gasoline) engines.
Get back
Air fuel ratio calculator
| ma [1000] | Fuel type | λ [-] |
| mf [thousand] | ηλ [%] |
Observation: The combustion efficiency is just calculated for diesel fuel and gasoline (petrol) fuel, using equations (4) and (5). For the other fuels, the combustion efficiency calculation is not available (NA).
Go dorsum
Affect of air fuel ratio on engine emissions
Internal combustion engine frazzle gas emissions depend heavily on the air fuel ratio (equivalence cistron). The main exhaust gas emissions in Water ice are summarised in the table below.
| Exhaust gas emission | Description |
| CO | carbon monoxide |
| HC | hydrocarbon |
| NOx | nitrogen oxides |
| Soot | unburnt fuel particles |
For a gasoline engine, CO, HC and NOx exhaust gas emissions are heavily influenced past air fuel ratio. CO and HC are mainly produced with rich air fuel mixture, while NOx with lean mixtures. So, there in no stock-still air fuel mixture for which we tin obtain the minimum for all exhaust emissions.

Image: Gasoline engine goad efficiency function of air fuel ratio
A three way goad (TWC), used for gasoline engines, has the highest efficiency when the engine operates in a narrow ring around stoichiometric air fuel ratio. The TWC converts betwixt l … 90 % of hydrocarbons and ninety … 99 % of carbon monoxide and nitrogen oxides, when the engine runs with λ = ane.00.
Go back
Lambda closed-loop combustion control
In guild to meet the exhaust gas emissions regulations, it is critical for internal combustion engines (especially gasoline) to take an authentic control of the air fuel ratio. Therefore, all of the mod internal combustion engines have airtight-loop control for air fuel ratio (lambda).

Epitome: Internal combustion engine closed-loop lambda control (gasoline engines)
- air mass flow sensor
- primary goad
- secondary catalyst
- fuel injector
- upstream lambda (oxygen) sensor
- downstream lambda (oxygen) sensor
- fuel supply circuit
- intake manifold
- exhaust manifold
The critical component for the system to work is the lambda (oxygen) sensor. This sensor measures the level of oxygen molecules in the exhaust gas and sends the information to the engine electronic control unit (ECU). Based on the value of the oxygen sensor reading, the gasoline engine ECU will adjusts the level of fuel mass in order to go along the air fuel ratio around the stoichiometric level (λ = 1.00).
For example (gasoline engines), if the level of oxygen molecules is to a higher place the threshold for stoichiometric level (therefore nosotros take a lean mixture), at the next injection cycle, the injected fuel amount will be increased in order to make use of the backlog air. Conduct in mind that the engine will always transition from lean mixture to rich mixture between injection cycles, which will give an "average" of stoichiometric air fuel mixtures/ratio.
For diesel engines, since it always runs on lean air fuel ratio, lambda command is performed in a dissimilar manner. The end goal beingness all the same the aforementioned, control of the exhaust gas emissions.
For whatever questions or observations regarding this tutorial please use the comment form below.
Don't forget to Like, Share and Subscribe!
Source: https://x-engineer.org/air-fuel-ratio/





0 Response to "what is the best fuel to air ratio?"
Post a Comment